GeoGebra für Schüler: Mathematik verstehen mit interaktiven Grafiken & 3D-Plots

/ Lernhilfen / Nachhilfe-Tipps, Mathematik-Software / Von

GeoGebra ist mehr als nur eine Geometrie-Software. Mit diesem kostenlosen Tool lassen sich Funktionen, Gleichungen und 3D-Objekte interaktiv darstellen – ideal für Schüler, Abiturienten und Studenten. In diesem Artikel zeige ich dir, wie GeoGebra im Unterricht und beim Selbstlernen hilft und welche Features besonders nützlich sind.

GeoGebra im Unterricht und für Schüler

GeoGebra ist ein interaktives Mathematik-Programm, das Schülern das Verständnis von abstrakten Konzepten erleichtert. Es unterstützt:

  • Geometrie: Punkte, Strecken, Kreise, Dreiecke und Transformationen
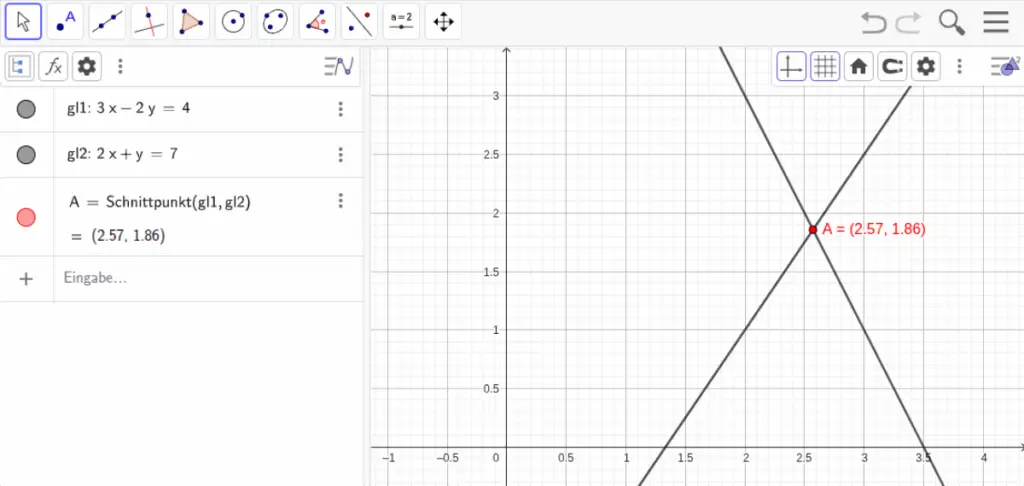
  • Algebra: Gleichungen, Funktionen und lineare Systeme
  • Analysis: Ableitungen, Integrale und Funktionsgraphen
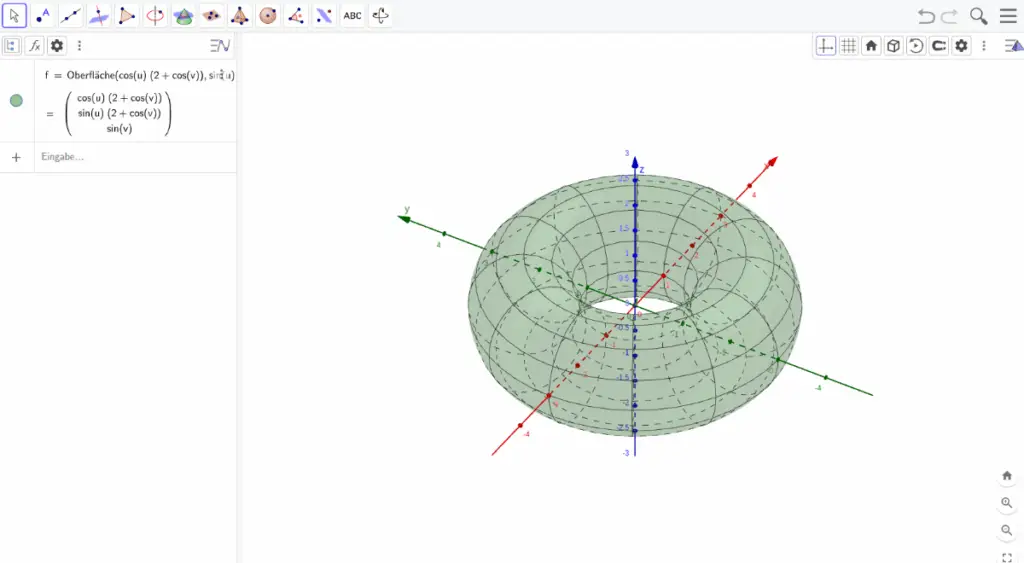
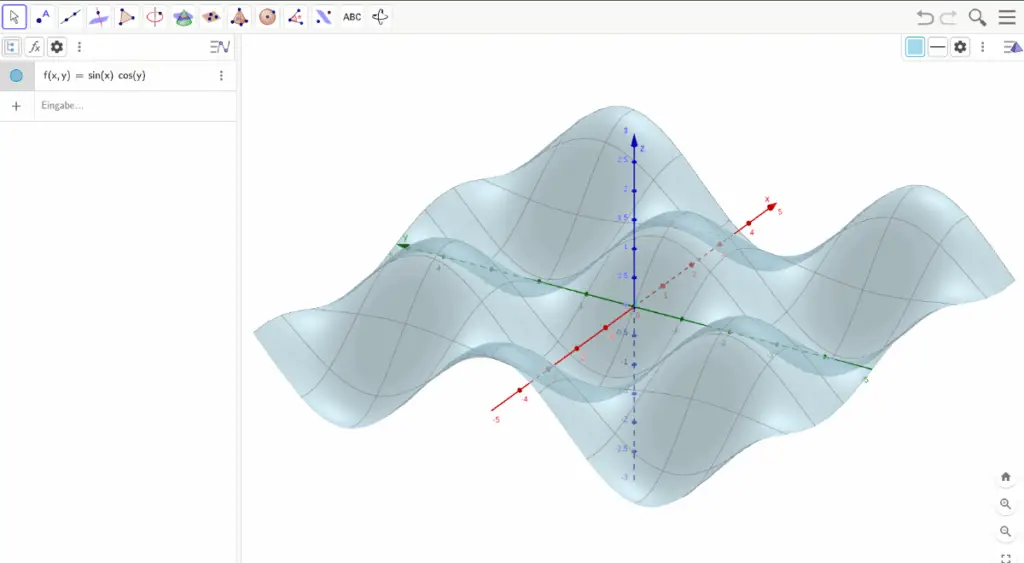
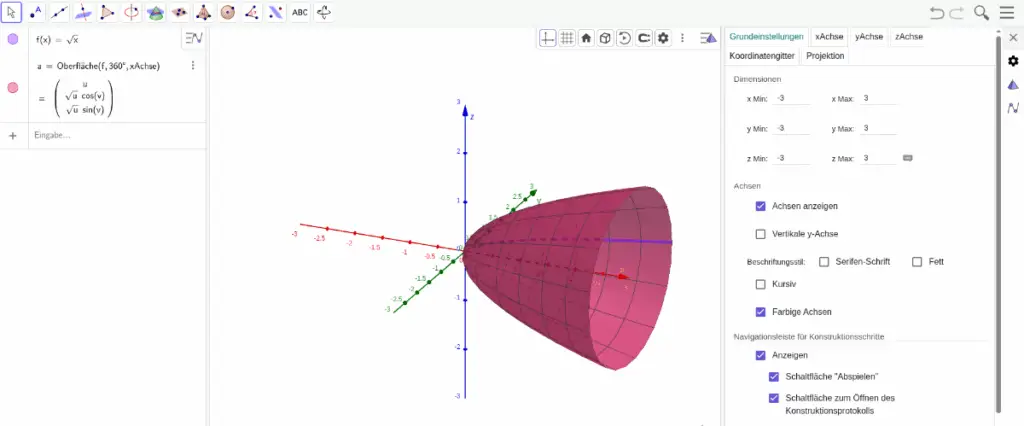
  • 3D-Darstellung: Flächen, Körper und Volumen

Die Software ist webbasiert, für Desktop und Tablets verfügbar und kostenlos für Schüler und Lehrer.

Konkrete Beispiele

Um GeoGebra effektiv zu nutzen, zeige ich zwei typische Anwendungen:

Beispiel 1: Gleichungssystem lösen
2x + y = 7
3x - 2y = 4
Ergebnis in GeoGebra: x = 18/7, y = 13/7
Beispiel 2: 3D-Plot
Surface: z = sin(x) * cos(y), x ∈ [-5,5], y ∈ [-5,5]

Warum GeoGebra?

GeoGebra verbindet visuelles Lernen mit rechnerischer Genauigkeit. Schüler können durch interaktive Grafiken mathematische Zusammenhänge schneller begreifen.

Vorteile:

  • Kostenfrei und plattformübergreifend
  • Interaktive 2D- und 3D-Darstellungen
  • Ideal für den Nachhilfeunterricht oder Selbststudium
  • Große Community und vorgefertigte Materialien verfügbar

GeoGebra herunterladen oder online nutzen:

  • Online direkt im Browser starten: GeoGebra Classic
  • Desktop-Version für Windows, macOS oder Linux: GeoGebra Download
  • Apps für Tablet oder Smartphone (iOS & Android) über App Stores verfügbar

Auf der GeoGebra Website kannst du sofort mit interaktiven Übungen und eigenen Projekten starten – ohne lange Installation.

Fazit:

GeoGebra ist ein unverzichtbares Tool für Schüler, die Mathematik anschaulich und interaktiv lernen möchten. Egal ob Geometrie, Algebra oder Analysis – GeoGebra erleichtert das Verständnis und macht den Unterricht praxisnah.

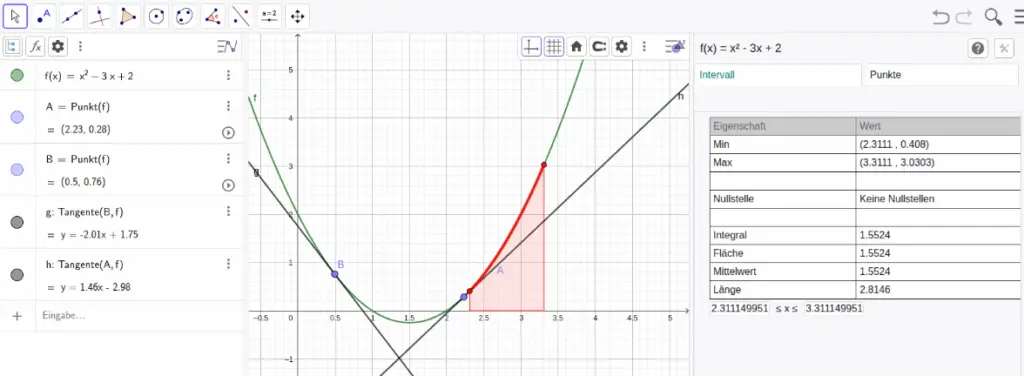
1. Screenshot & Mini-Tutorial: Funktionsgraph erstellen

Funktionsgraph erstellen:

  1. GeoGebra Classic öffnen (Online oder Desktop-Version)
  2. Im Eingabefeld die Funktion eingeben, z. B. f(x) = x^2 - 3x + 2
  3. Enter drücken → Funktionsgraph wird sofort angezeigt
  4. Mit der Maus Punkte auf der Kurve markieren oder Tangenten einzeichnen, um Eigenschaften zu erkunden

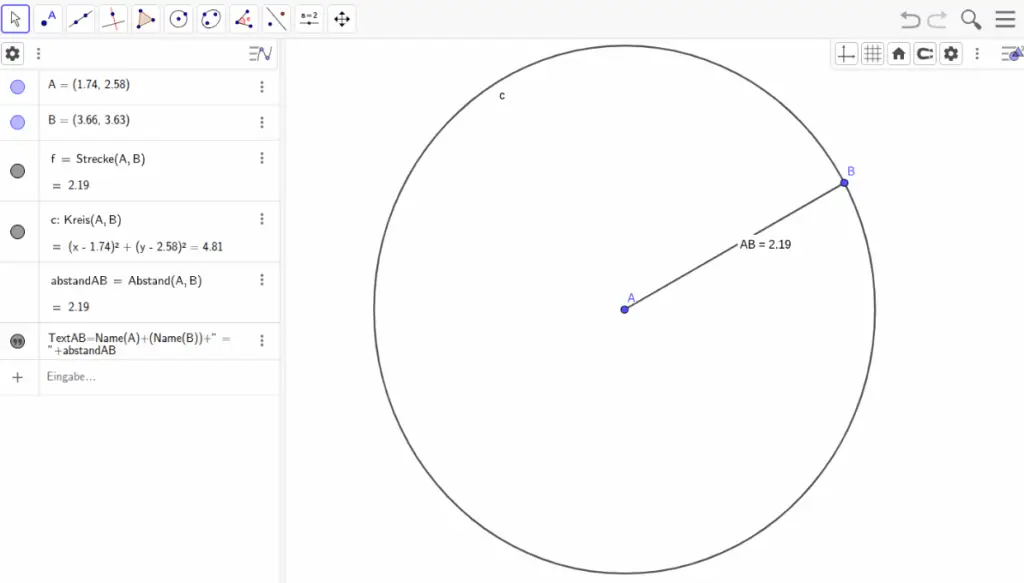
2. Screenshot & Mini-Tutorial: Geometrisches Objekt konstruieren


Geometrisches Objekt konstruieren:
  1. Punkte A und B setzen: Point[A] und Point[B]
  2. Strecke zwischen A und B zeichnen: Segment[A,B]
  3. Kreis um Punkt A mit Radius AB: Circle[A, B]
  4. Objekte verschieben, messen oder transformieren, um Eigenschaften zu entdecken

3. Screenshot & Mini-Tutorial: 3D-Plot erstellen

Rotationskörper erstellen:

  1. 3D-Ansicht aktivieren: Menü → Ansicht → 3D-Grafik
  2. Funktion eingeben, z. B. f(x) = sqrt(x)
  3. Rotationskörper erzeugen:
    Oberfläche(f,360°,xAchse)
  4. Den Körper interaktiv drehen und den Achsenbereich anpassen