Das Sekretärinnenproblem: Ein faszinierendes mathematisches Rätsel
Stell dir vor, du bist Chef eines Unternehmens und möchtest eine neue Sekretärin einstellen. Es gibt 100 Bewerberinnen, und du möchtest die Beste auswählen. Das Problem: Du musst jede Bewerberin sofort nach ihrem Vorstellungsgespräch entweder einstellen oder ablehnen, ohne die Möglichkeit, später zu einer zuvor abgelehnten Bewerberin zurückzukehren. Was wäre die beste Strategie, um die optimalste Kandidatin auszuwählen?
Dieses Dilemma wird in der Mathematik als das Sekretärinnenproblem bezeichnet. Es ist ein klassisches Beispiel aus der Wahrscheinlichkeitstheorie und Optimierung. Lassen wir uns Schritt für Schritt erklären, wie es funktioniert und wie man die beste Strategie entwickeln kann.

Das Grundprinzip des Problems
- Einzigartige Entscheidung: Du musst jede Bewerberin entweder sofort einstellen oder ablehnen. Du kannst keine späteren Kandidatinnen mehr mit den zuvor gesehenen vergleichen.
- Ziel: Die beste Bewerberin aus allen Kandidatinnen auszuwählen.
- Reihenfolge: Du siehst die Bewerberinnen nacheinander in zufälliger Reihenfolge.
Die mathematische Strategie
Mathematiker haben eine clevere Methode entwickelt, um die Chancen zu maximieren, die beste Bewerberin zu finden. Diese Methode basiert auf einer Kombination aus Beobachtung und Entscheidung:
- Beobachtungsphase: Du beginnst, indem du die ersten 37% der Bewerberinnen nur beobachtest und keine von ihnen einstellst. Bei 100 Bewerberinnen wären das die ersten 37 Kandidatinnen.
- Entscheidungsphase: Nach der Beobachtungsphase beginnst du, die restlichen Bewerberinnen zu beurteilen. Du stellst diejenige ein, die besser ist als alle, die du bisher gesehen hast.

Warum 37%?
Die Zahl 37% stammt aus der mathematischen Berechnung, bei der die eulersche Zahl e eine Rolle spielt. Der Wert 1/e (etwa 0,368) zeigt, dass die optimale Beobachtungsphase etwa 37% beträgt. Die eulersche Zahl e (ungefähr 2,718) ist eine fundamentale Konstante in der Mathematik und tritt in vielen Bereichen der Analysis und Wahrscheinlichkeitstheorie auf. Diese Strategie maximiert die Wahrscheinlichkeit, die beste Bewerberin auszuwählen, und die Erfolgschance liegt bei etwa 37%.
Ein einfaches Beispiel
Angenommen, du hast nur 10 Bewerberinnen:
- Beobachtungsphase: Du beobachtest die ersten 4 Bewerberinnen (etwa 37% von 10).
- Entscheidungsphase: Danach wählst du die erste Bewerberin, die besser ist als alle zuvor gesehenen.
Diese Strategie erhöht deine Chancen, die beste Bewerberin zu finden, erheblich, verglichen mit zufälligem Auswahl oder anderen naiven Ansätzen.
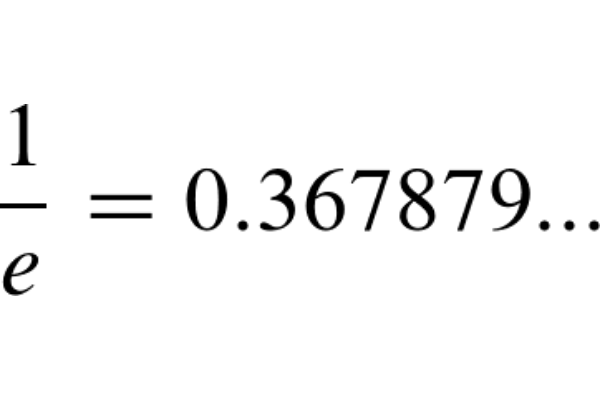
Fazit
Das Sekretärinnenproblem zeigt, wie Mathematik uns helfen kann, Entscheidungen unter Unsicherheit zu treffen. Obwohl das Szenario etwas theoretisch klingt, finden ähnliche Prinzipien auch in der realen Welt Anwendung, zum Beispiel bei Online-Dating, Auktionen oder sogar bei der Wohnungssuche. Es verdeutlicht, wie durch kluge Strategien und ein wenig Mathematik die Chancen auf optimale Entscheidungen verbessert werden können.
Nächstes Mal, wenn du vor einer Reihe von Entscheidungen stehst, denk an das Sekretärinnenproblem und die 37%-Regel – vielleicht hilft es dir, die beste Wahl zu treffen!