In dieser Aufgabe wickeln wir einen Faden gleichmäßig um einen Zylinder und wollen herausfinden, wie lang der Faden insgesamt ist. Solche Aufgaben sind klassische Geometrie-Beispiele und lassen sich mit dem Satz des Pythagoras elegant lösen.
Aufgabenstellung
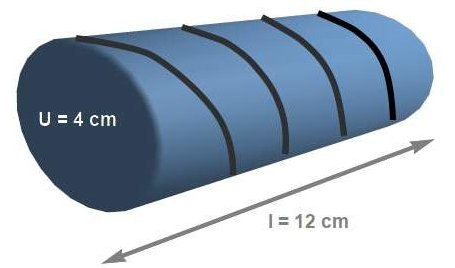
Ein Faden wird gleichmäßig schraubenförmig um eine Rolle gewickelt. Er reicht genau viermal um die Rolle herum. Die Rolle ist ein Kreiszylinder mit 4 Zentimetern Umfang und 12 Zentimeter Länge. Wie lang ist der Faden?
Lösung
Lösung
Veranschaulichung mit Papiermodell
Der rechnerische Ansatz lässt sich anhand eines Modells aus Papier veranschaulichen auf das man den Verlauf des Fadens mit einem Stift aufzeichnet.
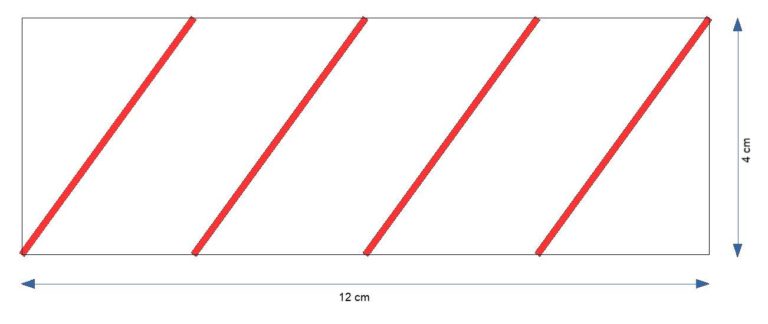
Wenn man dieses Papiermodell längs aufschneidet, erhält man das Netz des Zylinders als Rechteck.
Die Länge des Fadens entspricht der Summe der diagonalen roten Linien, die man auch als Hypotenuse von vier gleichartigen rechtwinkligen Dreiecken verstehen kann.
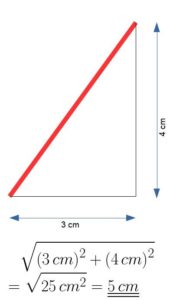
Wir können deren Länge also mit dem Satz des Pythagoras berechnen.
Die Länge der vertikal gezeichneten Seite entspricht dem Umfang des Zylinders aus der Aufgabenstellung.
(Kathete1 = 4 cm)
Die Länge der horizontalen Seite erhält man, indem man die Länge des Zylinders durch die Anzahl der Wicklungen teilt.
(Kathete2 = 3 cm)
Die Länge der roten Seite beträgt somit nach Anwendung des Pythagoras 5 cm.
(Hypotenuse = 5 cm)
Antwort:
Die Gesamtlänge des Fadens entspricht in unserer Aufgabe viermal der Länge der Hypotenuse und beträgt somit 20 cm.